整數關系探測算法是零誤差計算的算法基礎。事實上，整數關系問題最早可被追溯到歐幾里得時代。歷史上，Jacobi、Hermite、Poincaré等著名數學家都曾試圖給出有效算法，直到1977年由兩位美國數學家Ferguson和Forcade給出了一個可行的方法。在此基礎上，Ferguson 和 Bailey 給出的改進算法PSLQ被廣泛應用于計算數論、計算物理、實驗數學等領域，被喻為“20世紀十大算法之一”(SIAM News 33(4):1-2, 2000)。然而，在實際計算中，該算法依賴于高精度的浮點運算，其數值穩定性及計算復雜度等問題自上世紀七十年代被提出以來，一直懸而未決。重慶研究院近期的這項工作解決了PSLQ算法的數值穩定性問題，為進一步解決數值PSLQ算法的計算復雜度問題提供了良好的理論工具。審稿人評價為“… The results are definitely new – this reviewer is not aware of any other similar results.”

　　通過對原始算法的重新分析，新發現了算法中的一個不變關系。基于這一關系，該研究給出了改進算法，給出并證明了改進算法的新的終止條件。以此為基礎，對算法進行擾動分析，揭示了輸入數據精度與輸出質量的內在關系，從而建立了如下的前向誤差定理：

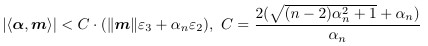
　　該定理能夠很好地解釋大量實驗數據所顯示出的規律，為數值PSLQ算法的設計與分析奠定了理論基礎。該項研究獲得國家自然科學基金項目、中科院前沿科學重點研究項目、中科院青促會項目的支持。

　　論文鏈接：  

　　http://www.ams.org/journals/mcom/0000-000-00/S0025-5718-2018-03356-7/